HF Rechner

  Last Update May 1st 2024


Allgemeine Aufgaben

---

Frequenz zu Wellenlänge

Umwandlung Frequenz zu Wellenlänge Freq. [MHz]       Velocity-Faktor [/]       Wellenlänge λ [m] 1 λ in Vacuum             1 λ in Medium         - - - Brüche: 1/4 λ in Vacuum             1/4 λ in Medium         1/2 λ in Vacuum             1/2 λ in Medium         3/4 λ in Vacuum             3/4 λ in Medium

Mathematik und Physik hinter diesem Rechner?

•      Wellenlänge in Vacuum:  λ = c / Frequenz

Lichtgeschwindigkeit c = 299 792 458 m/s im Vacuum

Eine Wellenlänge λ in einem Medium verschieden vom Vacuum wird beschrieben durch

•      Wellenlänge λ = (c x Velocity-Faktor) / Frequenz

Der Velocity-Faktor v ist eine Funktion von , der relativen Dielektriziätszahl oder Permittivität eines Medium. Sie beschreibt, wie schnell eine Welle in einem Medium fortschreitet und ist damit direkt verknüpft mit der Änderung der Wellenlänge in diesem Medium.

(Vacuum) = 1.00000 => v = 1.0000
(Luft)        = 1.00059 => v = 0.9997

Bitte beachten: Durch die Frequenzabhängigkeit des und so auch des V-Faktors der Plastikisolation von Koaxialkabeln muss für den VHF/UHF-Bereich in der Regel noch 5 bis 7 Prozent vom Ergebnis dieses Rechners an Länge abgezogen werden. Die Hersteller geben den V-Faktor zumeist bei etwa lediglich 1 MHz an.

---

EIRP : Äquivalente isotrope Sendeleistung

EIRP Rechner Watt an Ant.      Ant. Gain [dBi] EIRP in W          und kW

Um was geht es bei EIRP?

Der Term EIRP wird oft in Zusammenhang mit EMV (Elektromagnetische Verträglichkeit) und Strahlungsleistung elektromagnetischer Felder benutzt. Einfach gehalten steht EIRP für das Äqivalent aus in einen isotropen Strahler (Gewinn = 0 dBi) gespeister Leistung als normiertert Bezugswert für anderem als isotrope Antennen mit deren eingespeister Leistung. Durch diesen Bezug können richtungsbezogene Leistungspegel z.B. in Hauptstrahlrichtung einfach verglichen werden. Für Funkamateure kann der Vergleich der Leistung zweier Stationen interessant sein. Nehmen wir einen DX - Aufbau für 70 cm an: Eine Station speist 700 W in eine Antenne mit 17,1 dBi, die andere 400 W in eine mit 19.8 dBi. Welche von beiden "pumpt" mehr Strahlungsleistung in Hauptstrahlrichtung?

Welche Formeln stecken hinter diesem Rechner?

1. Umwandlung vom Isotropem Gewinn der Antenne zu reinem Zahlenwert

2. EIRP wird errechnet durch Multiplikation von Leistung in Watt mit numerischen Gewinn der Antenne gegen den isotropen Strahler

'Gewinn,iso' = dBi = dBd + 2.15 dB. Beispiel: 12.10 dBd ist 14.25 dBi

---

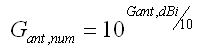
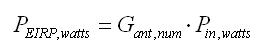
Umrechnung von Watt zu dBm & dBm zu Watt

W > dBm W   >     dBm                     dBm > W dBm   >     W

dBm ist Dezibel-Milliwatt, es referenziert Leistung zu einem mW - mit 0 dBm = 1 mW

•    0 dBm = 0.001 W
•  10 dBm =   0.01 W
•  50 dBm =   100 W

Welche Formeln stecken hinter diesem Rechner?

---

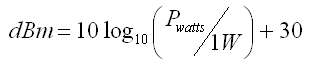
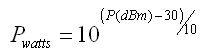
dB Umwandlungsrechner

Gewinn, numerisch > dB Gain [num.]   >     Gain [dB] Gain, dB > numerisch Gain [dB]   >     Gain [num.]

Diese Umwandlung funktioniert mit GEWINN und VERLUSTEN:
• Gewinn  3.0 dB = 2.00 numerisch
• Gewinn     0 dB = 1.00 numerisch
• Gewinn -3.0 dB = 0.50 numerisch

Welche Formeln stecken hinter diesem Rechner?

Ein Gefühl für den numerischen Wert des Gewinns als mit Zahlenwert multiplizierter Leistung in Watt bekommen, siehe EIRP - Rechner:
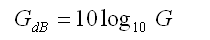
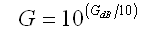
• x 2.00 numerisch = Wir wissen, dass ein Gewinn von 3 dB doppelte Ausgangsleistung ergibt
• x 1.00 numerisch = Addieren von 0 dB führt zu keiner Änderung
• x 0.50 numerisch = ist halbe Ausgangsleistung

---

Verstärkungsgewinn oder Abschwächung zu Watt ein / aus Rechner

Watt ein, Gewinn oder Verlust zu Watt am Ausgang Watts input   >     Gain/(-)Loss [dB]         Watts out [W]

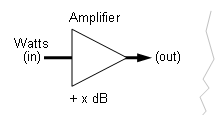
Welche Formeln stecken hinter diesem Rechner?

Leistungspegel in dB können addiert (Gewinn) oder subtrahiert (Verlust) werden.
Also überführen wir Eingangsleistung in Watt in Leistungspegel (dB) bezogen auf 1 Watt (dBw)

Als nächstes addieren wir die Leistungspegel von eingespeister Leistung und des Verstärkerblocks bzw. Abschwächers

Generalisiert für eine Kette von Verstärker- und Abschwächungsblöcken sieht die Formel so aus:
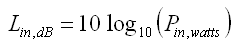
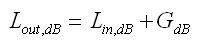
Beachte die sehr explizite Schreibweise "Loss_x". Allgemein wäre das eine weiter Verstärkerstufe mit Gewinn < 1.00



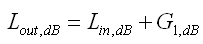
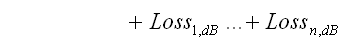
Schließlich überführen wir den Leistungspegel (dB) zurück in Watt

---

Temperatur zu dB Rechner

Kelvin zu dB Rechner Kelvin [K]         dB oder NF

Welche Formeln stecken hinter diesem Rechner?

mit To = 290 K = 17° Celsius mittlere Umgebungstemperatur (273 K = 0° C)

---

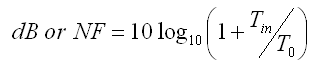
Und umgedreht ... dB zu Kelvin Rechne

dB zu Kelvin Rechner dB oder NF         Temp. [K]

Welche Formeln stecken hinter diesem Rechner?

mit To = 290 K = 17° Celsius mittlere Umgebungstemperatur (273 K = 0° C)

---

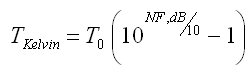
μV zu dBm Rechner

μV to dBm Calculator μV         Ohm         Berechnete dBm

Welche Formeln stecken hinter diesem Rechner?

dBm ist Leistungspegel bezogen auf 1 mW

---

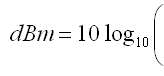
dBm zu NF Rechner      Empfängerempfindlichkeit zu Rauschmaß (Noise Figure)

dBm zu NF Rechner dBm         BW (kHz)         S/N (dB)         dB oder NF

• BW = Bandbreite
• dBm = Leistungspegel bezogen auf 1 mW
• To = 290 K oder 17° C Umgebungstemperatur

Benutzung dieses Rechners mit Spezifikationen aus dem Datenblatt des Empfängers

Da unterschiedliche S/N Verhältnisse wie Bandbreiten benutzt werden, sollten diese
zusammen mit dem für die Empfindlichkeit angegebenen μV oder dBm im Datenblatt
nachgeschlagen und in den Rechner eingegeben werden, um ein korrektes Ergebnis zu erhalten.

Typische Werte

• nominale BW's: CW oder in SSB = von 2.4 ...3 kHz, AM = 6 kHz, FM = 12.5 ... 25 kHz
• CW Filter? => wie Bandbreite des Filters
• nominales S/N = 6, 10 oder 12 dB


Welche Formeln stecken hinter diesem Rechner?

k = Boltzman-Konstante (1.3 x 10-23 J/K)

---

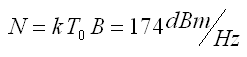
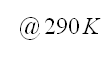
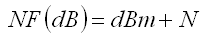
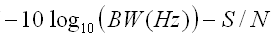
SNR to S-Units and μV Calculator

Enter in dBm IARU Region 1 rec. for Base Level Short Wave = -121 dBm, VHF and up: -141 dBm Base level       Noise Floor       Signal SNR   dB S-Units, absolute    /    plus dB S-Units, relative to noise floor    /    plus dB Volts at 50 ohms   μV

---

G/T Rechner

G/T - Verhältnis Gewinn (dBi)         Temp. (K)         Errechnetes G/T (dB)

Welche Formeln stecken hinter diesem Rechner?

---

VSWR & Anpassungsverlust (Mismatch Loss)

Z1 kann Zo oder 'an Transmitter oder Receiver' sein
und Z2 kann z.B. die Impedanz am Speisepunkt der Antenne sein.

Das "Mismatch Loss" (ML) drückt die Verluste durch Verbinden verschiedener Impedanzen aus

VSWR & Mismatch Loss Z1(Ω)         Z2(Ω) = R + j         Z2 absolut        (Ω) VSWR           ( / ) Refl.-koeffizient Γ   ( / ) Return Loss    (dB) Mismatch Loss (dB)

Anwendungsbeispiel zum Mismatch Loss :

Eine gegebene 50 Ohm Speiseleitung von 10 m Länge mit einem Leitungsverlust von 1,2 dB soll an eine Antenne von 75 Ohm angeschlossen werden. Wie groß ist der Gesamtverlust?

Der Rechner zeigt ein Mismatch Loss von -0,177 dB, das Kabel bringt weitere 1,2 dB = der Gesamtverlust geträgt hier 1,377 dB.


Welche Formeln stecken hinter diesem Rechner?

Z2 in absoluten Zahlen entspricht

damit machen wir den Rest wie folgt

---

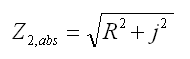
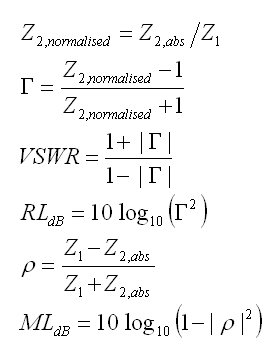
73, Hartmut, DG7YBN