Boom [mm]       144 MHz       432 MHz
25 x 25 mm      3.7 mm        7.1 mm 

---

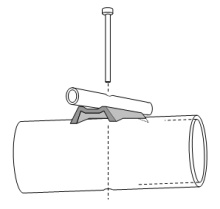
6. Von VE7BQH veröffentlichte Werte

             

Gilt für leitend auf den Boom mit Haltern aus gebogenem Metallblech angebrachte Elemente.
Man beachte die Länge dieser Halter, denn diese ist hier ein sehr wichtiger Parameter! Die untenstehenden Werte sind nur für 144 MHz gültig.

     Aus der 144 MHz VE7BQH G/T Tabelle, Ausgabe 75 - 25. April 2010

    "CORRECTION FACTOR FOR CUSHCRAFT AND CUDEE STYLE MOUNTED ELEMENTS

    CUSHCRAFT CORRECTION FACTOR ON 2 METERS = .3125" OR 7.94MM
    CUDEE CORRECTION FACTOR ON 2 METERS     = .2500" OR 6.35MM"

---

Online DL6WU / G3SEK Boom Correction Rechner

Beachte den doppelten Output (1) für Bauen mit Isolierteilen durch den Boom und (2) für elektrisch leitende Montage durch den Boom

DL6WU/G3SEK Boom Correction Bitte Werte eingeben Freq. [Mhz]         Boom Dim. [mm]     Berechnete Boom-Korrektur bei Wellenlänge [m] Isoliert durch den Boom [mm]                     Leitend durch den Boom [mm]

Achtung!   Bitte den passenden Segmentation-BC (SBC) für NEC-Modelle mit hoher Segmentierung aufschlagen, außer für LFAs, Quads und Quagis. Mehr über Boom Correction und Segmentierung von NEC Modellen weiter unten - klick.

Details zum DL6WU BC siehe weiter unten.

---

Bauart mit leitend durch den Boom angebrachten Elementen

Die DL6WU / G3SEK Formel liegt in zwei Versionen und einigen Abwandlungen davon vor.
Aber wie auch immer - über die brauchbare Anwendungsbreite liefern alle ein identisches Ergebnis.

Die Bezeichnung Preßpassung (engl. "Press fit") in der Skizze meint einen dauerhaften guten elektrischen Kontakt. Es sei denn, jemand ist fähig eine sehr kleine Schweißnaht zwischen Element und Boom zu legen, finden wir diese Bauart nur für Mikrowellenbänder (siehe unten), wo die kurzen Elemente mit einem Hammer in den Boom getrieben werden. Es gibt kommerziell gefertigte Aufbauten, die sich eines "semi leitend durch den Boom" - Baustils bedienen, wie Antennes Tonna oder Flexa-Yagi. Hier werden die Elemente auf den Boom geklammert oder geschraubt. Da der dadurch erreichte elektrische Kontakt relativ labil erscheint, benötigen diese Yagis entweder ein "verzeihendes" Breitbanddesign - oder ihre Leistung wird sich mit der Zeit verschlechtern.


1. Aus G3SEK's Long Yagi Workshop:

Aus dem Englischen von DG7YBN. Der originale Wortlaut findet sich auf meiner englischen Seite .. oder natürlich bei G3SEK.

    "Eine geeignete Formel zur Boomkorrektur ist:

    BC = [733 * BD * (.055 - BD)] - [504 * BD * (.03 - BD)]

    wobei BC die Korrektur als Bruchteil des Durchmessers des Boom BD angibt (beide mit
    der Wellenlänge als Einheit). Die Korrektur des Boom-Effekts muss immer zu der
    unkorrigierten Länge des Elements addiert werden. [...] Diese Formel ist aus den
    experimentellen Arbeiten von DL6WU hergeleitet und gilt für Elemente, die durch
    einen runden Boom laufen."

    C = 25.195 * B - 229 * B^2

    C = Boomkorrektur als Bruchteil des Durchmessers des Boom B, beide in [wl] => [ / ]
    B = Boom-Durchmesser   [wl]
    ^2  bedeutet zum Quadrat, 10^6 bedeutet 10 "hoch" 6

    C/B = 25.195 * (B/λ) - 229 * (B/λ)^2

    "... wobei C die Korrektur und B der Durchmesser des Booms sind, beide in Millimetern."
    [C/B = Verhältnis - Korrekturlänge zu Durchmesser des Booms in Wellenlängen]

BC = [25,195 - 229 * BD/(λ*1000)] * [BD/(λ*1000)]^2 * λ*1000

BC = Boom-Korrektur        [mm]
BD = Durchmesser des Boom  [mm]
λ  = Wellenlänge           [m]

c = 299.792.458 m/s
λ = c/f[Hz]  =>  in SI Einheiten   =  [ms]/[1/s] = [m]
Für einfache Handhabung benutze man für die Frequenz in MHz * 10^6 = Hz = 1/s

Zur Beachtung 1: Die Formel liefert ab einem Boom-Durchmesser größer 0.055 Lambda keine exakten Werte mehr
Zur Beachtung 2: Diese Formeln gehen weder auf den Durchmesser der Elemente, noch deren Länge ein.

---

Bauart mit isoliert durch den Boom geführten Elementen

1. Die DL6WU / G3SEK Formel in klassischer Schreibweise

    C = 12.5975 * B -114.5 * B^2

    C = Boomkorrektur als Bruchteil des Durchmessers des Boom B, beide in [wl] => [ / ]
    B = Boom-Durchmesser   [wl]
    ^2  bedeutet zum Quadrat, 10^6 bedeutet 10 "hoch" 6 

    BC = (12.5975 - 114.5 * B) * B^2

    BC = Boom-Korrektur  [wl]
    B = Boom-Durchmesser [wl]

BC = [12,5975 - 114,5 * BD/(λ*1000)] * [BD/(λ*1000)]^2 * λ*1000

BC = Boom-Korrektur   [mm]
BD = Boom-Durchmesser [mm]
λ  = wavelength       [m]

c = 299.792.458 m/s
λ = c/f[Hz]  =>  in SI units  =  [ms]/[1/s] = [m]
Für einfache Handhabung benutze man für die Frequenz in MHz * 10^6 = Hz = 1/s

Boom Dim.       144 MHz       432 MHz
15 x 15 mm        n.a.          n.a.
20 x 20 mm      2.0 mm        5.0 mm
25 x 25 mm      3.0 mm        6.0 mm
30 x 30 mm      5.0 mm        7.0 mm
35 x 35 mm      6.0 mm          n.a.
40 x 40 mm      8.0 mm          n.a.

Elemente Ø 4 mm (Schweißstäbe aus Aluminium), Ø 6 mm Löcher im Boom,
Nylonnieten Typ 61PR800000 (ohne Ruß als Füllstoff), Heyman Manufacturing GmbH, D-35390 Gießen
BTW: DL6WU schreibt mir: "Die Methode "Nylonnieten" hat nicht DJ9BV erfunden, er hat sie von mir übernommen und ich habe sie von DJ6NS"

In englischen Maßeinheiten

Boom Dim.                144 MHz       432 MHz
Ø 0.630" / 16.0 mm          n.a         3.67 mm
Ø 0.750" / 19.1 mm       2.02 mm        4.94 mm
Ø 0.875" / 22.2 mm       2.69 mm        5.00 mm
Ø 1.000" / 25.4 mm       3.47 mm        7.00 mm
Ø 1.125" / 28.6 mm       4.32 mm        9.00 mm
Ø 1.250" / 31.8 mm       5.25 mm       10.69 mm
Ø 1.375" / 34.9 mm       6.25 mm       11.64 mm
Ø 1.500" / 38.1 mm       7.32 mm         n.a.
Ø 1.750" / 44.6 mm       9.63 mm         n.a.
Ø 2.000" / 50.8 mm      12.15 mm         n.a.

Metrische Maßeinheiten

Boom Dim.                144 MHz       432 MHz
Ø   n.a  / 20.0 mm       2.21 mm         n.a.
Ø   n.a  / 38.0 mm       7.28 mm         n.a.

Boom Dim.                144 MHz       432 MHz
Ø 0.630" / 16.0 mm         n.a.          n.a.
Ø 0.750" / 19.1 mm         n.a.          n.a.
Ø 0.875" / 22.2 mm         n.a.         6.44 mm
Ø 1.000" / 25.4 mm         n.a.         8.12 mm
Ø 1.125" / 28.6 mm         n.a.         9.57 mm
Ø 1.250" / 31.8 mm         n.a.        11.43 mm
Ø 1.375" / 34.9 mm         n.a.        13.27 mm
Ø 1.500" / 38.1 mm         n.a.          n.a.
Ø 1.750" / 44.6 mm         n.a.          n.a.

Elemente Ø 3/16" = 4.76 mm, Löcher im Boom 5/8" ?
Runde Isolatoren aus PA, Fächerscheiben (engl: starlock washers) zur Elementbefestigung

Boom Dim.       144 MHz       432 MHz
Ø 15 mm           n.a           n.a.
Ø 20 mm        1.50 mm        5.7 mm
Ø 22 mm        1.75 mm        6.2 mm
Ø 25 mm        2.50 mm        7.7 mm
Ø 30 mm        4.00 mm       10.0 mm
Ø 35 mm        5.40 mm       12.8 mm
Ø 40 mm        7.00 mm       15.1 mm

Elemente Ø = 5 mm, Löcher im Boom 8 mm
M8 Schraube und Mutter aus schwarz gefärbtem Nylon (Delrin) mit Ø 5 mm Hohlschaft.

6. Zusammenfassung

Wen wir uns die Tabellen oben ansehen, fällt auf, das es zwischen den Werten einige Differenzen gibt. Das mag an den verschiedenen Details der Aufbauarten liegen. Die Größe der Löcher im Boom, Halter- oder Isolatorgeometrie und Material ... all die Details, die wir in dem reinen BC-Wert nicht mit angegeben finden, könnten dafür verantwortlich sein. Daher ist es ratsam, wenn man sich für eine der oben gezeigten Korrekturen entschieden hat, auch den zugehörigen Baustil zu benutzen.

Es geht noch weiter - SM5BSZ's BC.exe schließt die meisten der noch freien Parameter mit ein und sollte daher geeignet sein, den besten Wert von allen für isoliert durch den Boom geführte Elemente zu liefern.

---

BC.exe von SM5BSZ für isoliert durch den Boom geführte Elemente

BC.exe von Leif Åsbrink basiert auf präzisen Messungen, die auf Teilstücken aus Boomrohr und Elementen innerhalb einer
Resonanzkammer ausgeführt wurde. Die effektiven Paramater sind

1. Boom - Querschnittsform (0 = rund / 1 = quadratisch)
2. Außendurchmesser des Boomrohrs
3. Wandstärke des Boomrohrs
4. Durchmesser des Lochs zur Elementbefestigung
5. Durchmesser der Elemente
6. Länge der Elemente
7. Entfernung des jeweiligen Elements zum NÄHEREN Ende des Boomrohres

Alle Maße sind in Millimetern anzugeben

1. Eigene Daten in "INPUT.BC" eintragen
2. Die Datei unter Beibehaltung des Dateinamens im gleichen Ordner wie das BC.exe speichern
            ⇓
3. Die BC.exe aufrufen
            ⇓
4. Die BC-Längen der Datei "OUTPUT.BC" entnehmen

Unten steht als Beispiel eine "INPUT.BC" mit einer 7 Element Yagi.
Man beachte die letzte Spalte - diese enthält die Entfernung zum nächstgelegenen Boom-Ende.

Jetzt wird die BC.exe aufgerufen, sie verschwindet sofort wieder ... es brauchte mehrere Versuche einen Screenshot zu fassen
(Das Bild zeigt eine andere Datei).

Und so sieht dann die Ausgabedatei "OUTPUT.BC" aus

Das Editieren / Lesen von "INPUT.BC" wie "OUTPUT.BC" Dateien funktioniert prinzipiell mit jedem Textverarbeitungsprogramm. Ich benutze "Notepad++", aber Windows "Editor" reicht völlig aus. Das originale BC.exe berechnet nur für 144 MHz korrekte Werte.

Link zur SM5BSZ Webseite über BC.exe

Man öffnet die oben gezeigte INPUT.BC in einem neuen Browser-Fenster (tab), kopiert den Inhalt in eine .txt Datei und speichert in den gleichen Ordner wo auch die BC.exe liegt, benennt diese in INPUT.BC um und lässt diese durch das BC.exe laufen.

---

Modifiziertes BC.exe für die Verwendung auf anderen Frequenzen

Ein modifizierter Build der BC.exe für effektiv wirksame Eingabe der Berechnungsfrequenz, welcher aber bislang noch nicht an echten Messaufbauten verifiziert ist. Das ist der modifizierte und neu kompilierte Fortran Code mit korrigierter Skalierung, so wie eigentlich beabsichtigt. Diese Modifikation wurde von VE7BQH unter Konsultierung von SM5BSZ ausgeführt.

Eine INPUT.BC Datei für 432 Mhz für eine echte Langyagi

Und so sieht die OUTPUT.BC Datei aus

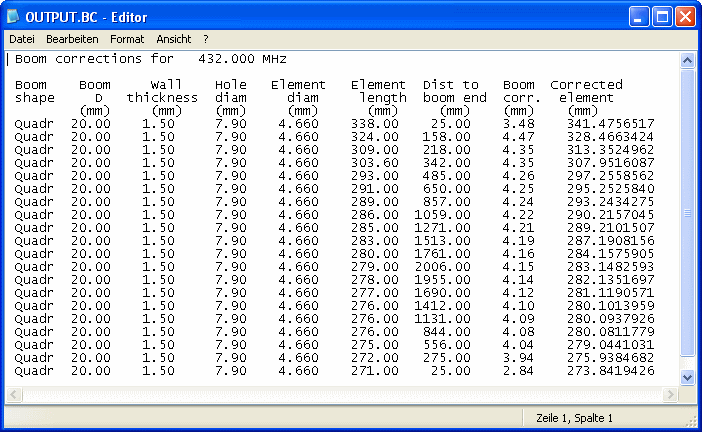
Download BC.exe modifiziert 32 Bit Vers. 3 als .zip Datei; inklusive einiger Beispiele in der "INPUT.BC" Datei und readme.txt. Download BC.exe modifiziert 64 Bit Vers. 1.0 als .zip Datei; inklusive Beispiel INPUT.BC Datei


Die 64 Bit Version läuft auf win7 und 8 und schreibt eine Datei namens "OUTERR.txt" die zeigt, warum BC.exe nichts berechnet bei falscher Eingabe. Die OUTERR - Datei ist eine von mir eingefügte Erweiterung, ebenso wie die Portierung auf Fortan 95 um das BC.exe in eine 64 Bit .exe zu compilieren.

Download Source Code des modifizierten BC.exe inklusive Schreiben der OUTERR - Datei


* Achtung: Dies modifizierte BC.exe ist außer für 144 MHz bis 432 MHz noch nicht für weitere Frequenzbereiche verifiziert *

Bitte beachten:
1. Dies modifizierte BC.exe ist bisher nur für 144 und 432 MHz an echten Yagis getestet
2. Plastikhalter, die groß sind in Relation zur Wellenlänge werden nicht von BC.exe kompensiert
3. Es wird keine Garantie gegeben auf BC.exe, wie auch immer, die Benutzung von BC.exe geschieht auf eigenes Risiko.
4. Leif Asbrink, SM5BSZ besitzt das alleinige Recht an BC.exe und dem Source Code dazu.

Die Beispiel-INPUT.BC Dateien beinhalten eine Reihe von Yagis und Testkonfigurationen. Jede ist durch eine freie Zeile abgetrennt. BC.exe stoppt die Berechnung an der ersten angetroffenen Leerzeile. Durch Kopieren des gewünschten Bereichs nach oben in der .txt-Datei direkt unterhalb der ersten Zeile, welche die Frequenzangabe enthält kann die INPUT.txt Datei aufbereitet werden. Noch Leerzeilen darunter einfügen und speichern. Nun kann mit Aufruf der BC.exe die Datei gerechnet werden.

---

UA3TZ's boom.exe - noch eine Korrektur, die den Einfluss der Boom-Enden einbezieht

Boom-e.exe ist ein DOS-Konsolenprogramm von Anatolij I. Grechikhin, UA3TZ

Die Theorie wurde in einem Artikel in РАДИО Ausgabe Nr. 9, 2002 vorgestellt.
Im Gegensatz zu den meisten bekannten Korrekturen nimmt es die Entfernung zu den Enden des Booms auch für auf dem Boom montierte Elemente mit auf. Der Output ist ein nicht einheitlicher Werte pro Element, wie wir es auch bei BC.exe von SM5BSZ finden, welches aber nur für isoliert durch den Boom geführte Elemente eine Korrektur errechnet.


Beispiel : 144 MHz 2.5 wl Yagi, nicht geleichförmige Boom-Korrektur nach UA3TZ

Hier sind 4 mm Elemente isoliert durch einen 20 mm Boom montiert, erstes & letztes Element in 20 mm Entfernung zum jeweiligen Ende des Booms. Man beachte die Abhängigkeit des BC-Wertes von der Position relativ zum näheren Ende des Booms. (das hier ähnelt vom Verlauf her stark dem, was SM5BSZ BC.exe rechnet, allerdings mit abweichenden Absolutwerten, siehe nächstes Kapitel))

Link zu einer externen Webseite mit UA3TZ's Artikel zu diese Boom-Korrektur .

Es rechnet für 3 Arten von Elementbefestigungen:

Arbeiten mit boom-e.exe

• Art 1, 2 oder 3 der Elementbefestigung auswählen & Enter
• Eintragen des Elementdurchmessers & Enter
• Eintragen des Boomdurchmessers & Enter
• Eintragen der Distanz zum näheren Ende das Booms & Enter
• Eintragen des Freiraums zwischen Oberfläche Boom und Element (nur für Typ #1 Elemente auf dem Boom) & Enter

Boom(-e).exe rechnet nur jeweils ein Element.
Für das nächste Elemente die "1" für Option '1 - other data' eingeben und den Rest wiederholen


Download  Link zur externen Download Webseite www.radioscanner.ru

Das Programm ist in zwei Sprachen beigefügt
boom-e.exe = Version in englischer Sprache
boom-r.exe  = Version in russischer Sprache

Tnx an Vladimir, UR5EAZ, der mich auf das Programm aufmerksam gemacht hat

---

Vergleich SM5BSZ BC.exe und UA3TZ boom(-e).exe

Beispiel: Elemente isoliert durch den Boom angebracht

432 MHz - Einfluss der Annäherung an die Enden des Boomrohres gerechnet mit BC.exe von SM5BSZ und boom(-e).exe by UA3TZ. Das Diagramm zeigt die Korrekturwerte für ein 340 mm langes Element in mm, für 20 x 20 x 2 mm quadratischen und Ø 20 mm runden Boom. Der Elementdurchmesser beträgt 4 mm, Elementlängen sind bei 340 mm eingefroren um eine Reihe von Vergleichswerten bei Variation der Entfernung zum näheren Ende des Booms zu erhalten.

Die Löcher im Boom von Ø 6 mm können Nylonnieten (DL6WU/DJ9BV) oder Plastikstopfen (DG7YBN) bzw. 6 x 4.00 mm Halter (7arrays) repräsentieren.

Vergleich DG7YBN Auf-rundem-Boom und UA3TZ boom(-e).exe

Für diesen Test nehme ich einen 30 mm Rundboom, 8,0 mm Elemente, 1,8 mm Freiraum zwischen Element und Oberkante Boom und variieren die Entfernung zum Ende des Booms für das hier sensitive boom.exe.

         

Wir müssen dabei in Betracht ziehen, dass der YBN On-Boom-BC mit den Haltern an Ort und Stelle ausgemessen wurde (v-Faktor des Plastik wirkt auf die das Element begleitende Länge ein) und es eine Schraube M3 durch Element und Boom gibt.

---

Ungleicher Betrag an BC je Element & Einfluss der Enden des Boomrohrs

In den Chats der Experten auf dem "moon net" und anderswo im Internet können wir ein großes Interesse am Thema, ob der BC adaptiv auf die Länge des einzelnen Elements erfolgen muss oder nicht, erkennen. Meiner Meinung nach müssen wir das Thema in zwei separate Fälle zerlegen, denn es sind zwei Mechanismen wirksam, die die BC-Werte der weit außen gelegenen Elemente erniedrigen können.

1. Betrifft nur isoliert durch den Boom montierte Elemente

Das BC.exe von SM5BSZ für isoliert durch den Boom montierte Elemente zeigt uns, daß es hier eine Abhängigkeit des BC von der Distanz des nächstgelegenen Boom-Ende gibt. Um ein paar Beispielwerte zu geben: Auf einem runden Boom bei 144 MHz beträgt die Verkürzung des BC-Wertes ungefähr 25% . Die Verkürzung startet sehr langsam ab einer Entfernung vom Ende von etwa 1 λ. Danach fällt sie mit zunehmender Annäherung an das Ende des Rohres rapide ab.

144 MHz, runder 25 mm Boom, nur grobes Beispiel!
Standard BC der Elemente in der Mitte des Booms ist 4.5 mm

Dist. zu Ende des Boom    Abnahme BC-Wert absolut
1.000 λ                   0.01 mm
0.150 λ                   0.20 mm 
0.014 λ                   1.10 mm              

Mathematisch ausgedrückt ergibt sich in etwa eine Abnahme dBC = 0,22 ln (Entfernung zum Ende) + 2,9), Zahlen in Millimetern. Allerdings ist das alles abhängig vom Innendurchmesser des Boom-Rohres, der Frequenz usw., ... siehe BC.exe, oben.

Der hier arbeitende Mechanismus ist, das das im Boom-Rohr eingeschlossen kleine Stück des Elements mit einem Bruchteil dessen, was außerhalb strahlt auch innen strahlt. Der innere Raum im Rohr bildet einen Hohlraum(resonator) mit verschiedenem Einfluss je näher wir an die Enden des Rohres gelangen. Das ist der Grund, warum BC.exe den inneren Boomdurchmesser über die einzugebende Wandstärke (Wall Thickness) einbezieht.

Beispiel 1: 432 MHz 19 Elem. Yagi (GTV 70-19m) - Einfluss der Annäherung an die Enden des Boomrohres gerechnet mit BC.exe von SM5BSZ. Aufgetragen ist die Korrektur der Elemente in Millimetern für 20 x 20 x 2 mm quadratisches Tragrohr. Dipol und Elemente besitzen einen Durchmesser von 4 mm. Die Isolatoren sind Nylonnieten (DL6WU/DJ9BV) oder Plastikendstopfen (7YBN) mit 6 mm Loch im Boom.
Zu sehen ist eine Überlagerung aus den Parametern (a) "Einfluss Elementposition zum näheren Ende des Booms" und (b) "Länge des Elements".

Beispiel 2: 432 MHz - Einfluss der Annäherung an die Enden des Boomrohres gerechnet mit BC.exe von SM5BSZ. Fiktives Bespiel um die Abhängigkeit Korrekturwert der Elementlänge vom näheren Ende des Booms deutlicher zu zeigen. Da auch die Elementlänge in BC.exe als Parameter in den Korrekturwert eingeht, ist hier die Länge der Elemente auf 300 mm festgehalten, um den Einfluss des Boom-Endes vergleichbar bzw. normiert wiederzugeben.

Beispiel 3: 432 MHz Yagi Elemente - Einfluss der Elementlänge bei ausreichend Abstand zu den Enden des Boomrohres gerechnet mit BC.exe von SM5BSZ. Aufgetragen ist die Korrektur der Elemente in Millimetern für 20 x 20 x 2 mm quadratisches Tragrohr für 4 mm Elemente Als Isolatoren kommen Nylonnieten (DL6WU/DJ9BV) oder Plastikendstopfen (7YBN) mit 6 mm Loch im Boom zum Einsatz.
Zu sehen ist die Veränderung des Boomkorrekturwertes über variierte Elementlänge als Parameter bei quasi fester Position auf dem Tragrohr.

  Tip!     Wer den Einfluss der Annäherung an das Ende des Boom weiter ergründen möchte, kann dies auf einfache Art mit dem MS Excel Yagi-Elemente Konfigurationswerkzeug selber tun. Einfach im SM5BSZ BC.exe Mode eine konstante Elementlänge eintragen und die Abstände zu den Enden des Booms hin auf immer kleinere Werte setzen. Dann über die Spalten Basis-BC und Position auf dem Boom ein Diagramm erstellen. Genauso sind auch die hier gezeigten Diagramme entstanden.     Link zum Werkzeug klick


2. Betrifft alle Arten von Elementmontagen

Das gleiche, wie oben aufgezeigt wird auch auf der Außenseite des endenden Rohres auftreten. Aber erst bei wesentlich kleinerer Entfernung. Das erste bzw. letzte Element der Antenne ist wesentlich weniger Einfluss ausgesetzt, wenn der Boom direkt nach der Elementposition geschnitten ist (also nichts übersteht). So sieht dies Element fast nur die Hälfte des "Boom-Volumens" das die anderen Elemente sehen. Seit wir uns dessen klar sind haben wir grundsätzlich bei allen Test-Yagis für den On-Boom-BC den Boom an beiden Enden um 30 bis 40 mm länger gelassen. Die veröffentlichten Analyse-Plots zeigen, dass das eine gute Idee war. Wenn die exakte End-Korrektur bekannt ist, kann man darauf verzichten, diese Überlänge auf den Boom einzubringen. Das BC.exe von SM5BSZ hat diesen Mechanismus wohl ebenfalls eingebunden.

---

Mikrowellen - Leitend durch den Boom

Boom Dim.       1296 MHz      2320 MHz
10 x 10 mm        n.a.         8.0 mm      DC3XY, DL6WU-Yagi for 2320 MHz, Dubus 4/1989
15 x 15 mm      11.0 mm         n.a.       DJ9BV, DL6WU Yagis for 23 cm, Dubus 2/1994
20 x 20 mm        n.a.          n.a.            

Traditionell werden die Elemente hier mit einem Hammer oder Presswerkzeug in den Boom geschlagen, so daß eine gute Preßpassung entsteht - welche aber noch mit einem Überzug mit Klarlack gegen Korrosion geschützt werden sollte.

Weitere Details

1. In DJ9BV's - "DL6WU Yagis for 23 cm" - Dubus 2/1994 finden wir Ø 4 mm Elemente aus Aluminium AlMgSi1, die in ein Loch von Ø 3.9 mm in einen Ø 15 mm Boom gepresst werden.

2. In DJ9YW's - "A Homebrew Yagi for 1296 MHz DX" - Dubus 1/2006 finden wir Ø 3.2 mm Elemente aus Aluminium AlMg5, die in Ø 3.1 mm Löcher in einem 15 x 15 x 1 mm Boom gepresst werden.

3. In DC3XY's - "DL6WU-Yagi for 2320 MHz" - Dubus 4/1989 finden wir Ø 2.4 mm Elemente aus AlMg3, die in Ø 2.3 mm hLöcher in einem AlMgSi 10 x 10 x 1 mm Boom gepresst werden.

"Don't try this at home" ... es sei denn, man hält sich strikt an die Daten und Geometrien wie in den Artikeln angegeben. Obwohl hier jeweils ein mehr oder weniger getesteter BC angegeben ist, rate ich dazu, nicht überoptimistisch zu werden. Aus gutem Grund sind die erwähnten Designs allesamt recht dankbare Entwürfe von oder nach DL6WU. Man sollte das nicht mit Designs mit hohem Q-Faktor versuchen, es sei denn man besitzt außergewöhnliche Erfahrung in Bauen und Ausmessen von Yagis und verfügt mindestens über einen Netzwerk-Analysator der das vorgesehene GHz Band überstreicht.

Alternativ können die Elemente in sicherer Höhe über dem Boom plaziert werden, indem Abstandsisolatoren benutzt werden, wie in den kommerziellen Beispielen der 1296 und 2320 MHz Tonnas und I0JXX Yagis zu sehen.

Man beachte, das das NEC2 Manual eine Passage enthält, in der es besagt, das ein Rohrende auf sehr hohen Frequenzen von weit über 432 MHz gegenüber einem Vollstab den Effekt einer kleinen Kapazität habe kann. Daher ist die elektrische Länge eines aus Rohr bestehenden Elements dadurch leicht verändert. Die genannten Größenordnungen sind leider recht vage. Aber ich denke, es ist sinnvoll darauf hinzuweisen.

---

Was die gute BC-Messungen beeinträchtigen kann

Eine Yagi kann in drei Zonen aufgeteilt werden

  1. Erregerzelle (engl.: Driver Cell)
  2. Wellenleitstruktur
  3. Übergangszone

  4. Symmetrier- und Transformationsglieder

Die meistverbreiteten Symmetrier- und Transformationsglieder sind aus Koaxkabel gemacht.

1. Das Koax richtig geschnitten bekommen

  Attenzione!

Es ist allgemein bekannt, das eine Länge Koaxkabel um dessen Verkürzungsfaktor verkürzt werden muss, wenn wir es auf eine bestimmte resonante Länge zuschneiden wollen. Die Geschwindigkeit einer Welle in einem Medium wird beschrieben durch

... oder multipliziert mit 100 ausgedrückt in % der Lichtgeschwindigkeit.
Nach IEC 60250 beträgt die Dielektrizitätskonstante von reinem PTFE εr = 2,1 (gemessen bei 1 MHz) oder v = 0.690 = 69%. Wie auch immer, Radioamateure benutzen zumeist v = 0.7... 0.71, so dass die berechnete Länge eines Viertelwellenstücks für 144 MHz etwa 369 mm entspricht.

Aber habt Ihr jemals die wahre Resonanzfrequenz des geschnittenen Stücks nachgemessen?
Auf VHF und darüber werdet Ihr wahrscheinlich erstaunt sein, dass der Stub in der Frequenz ungefähr 5...10% zu tief liegen wird. Das rührt daraus her, dass εr und Verkürzungsfaktor für eine viel niedrigere Frequenz spezifiziert worden sind und die dielektrischen Eigenschaften von Plastik zu einem gewissen Teil frequenzabhängig sind.

Von Links nach Rechts: DK7ZB Match, λ/2 Balun, Viertelwellenleitung

Die volle Wahrheit ist, dass Plastik eine so genannte "Dynamische Dielektrizitätskonstante" besitzt.

    M. Bonnet, Kunststoffe in der Ingenieuranwendung, Vieweg + Teubner, Wiesbaden 2009, pg. 73
    Chapter 1.7.1.3 Dynamic Dielectrical Constant and Dielectrical Loss

    "In einem elektrischen Wechselfeld werden die elektrischen Dipole gezwungen,
    mit der Frequenz ν des Wechselfeldes zu schwingen. Moleküle mit
    Orientierungspolarisation werden dabei gezwungen, jedes Mal ihre Richtung im
    Raum zu ändern. Dies führt zu einer Relaxationsdämpfung."

Es ist besagte Relaxationsdämpfung, welche die Dielektrizitätskonstante mit steigender Frequenz kleiner werden lässt,
weil sie die Wellengeschwindigkeit im Plastik mit zunehmender Frequenz weiter herabsetzt. Das lässt eben auch den
Zahlenwert des Verkürzungsfaktor absinken - und so die Länge unseres Koax-Stubs auf VHF und darüber.

  Auf der Seite Phasing & Matching Lines steht noch mehr dazu


2. Warum ist die exakte Länge von Koax-Balun oder Viertelwellenleitung so wichtig?

Weil jede überschüssige Länge unseres Anpassnetzwerks sich "virtuell" zur Spannweite des erregten Elements addiert. Ein Beispiel: Eine Viertelwellenleitung für 144,1 MHz aus PTFE Koax RG.142 B/U besitzt eine Länge von 369 mm, wenn sie nach allgemein angewandten V-Faktor von 0.7 berechnet wird. Die Länge der Leitung, wenn sie mit Hilfe eines Netzwerkanalysers sorgfältig auf Resonanz getrimmt wird ist 345 mm. Die 24 mm oder 7% an Überschusslänge beeinflussen das das VSWR, das wir für das komplette Arrangement aus Yagi plus Anpassnetzwerk messen.

Mehr über den Einfluss solcher Ungenauigkeiten kann man in meinem Artikel "Angewandte Umsetzung von Segmentierten
Drähten aus NEC in 144/432 MHz Yagi Elemente - Teil 3' in Dubus 2/11 nachlesen.

---

Boom-Korrektur und die Segmentierung des NEC Modells


Was passiert, wenn wir die Segmentierungsdichte der Elemente eines NEC Modells variieren?
Wir werden beobachten, wie sich der Resonanz-Peak in der Frequenz verschiebt. Die drei Plots unten zeigen die gleiche 2 m Yagi. Nur eben mit zunehmender Segmentierungsdichte von einem Plot der Rücklaufdämpfung (engl. Return Loss, RL) zum nächsten. Die Zahlen geben "stepped", also per Elementlänge gestufte Segmentierungsdichten an, wobei der Reflektor die meisten Segmente führt (Anfangswert) und dann fallend entlang der weiteren Elemente bis das letzte parasitäre und damit kürzeste Element erreicht wird. Auf diese Weise besitzt jedes Segment in etwa gleiche Länge, was in der besten Genauigkeit des Modells resultiert, die wir von NEC bekommen können.

5 Elem. DUT Yagi => 11 ... 9 Segmente (EZNEC Auto Segmentierung bei 144 MHz)

5 Elem. DUT Yagi => 16 ... 13 Segmente (EZNEC Auto Segmentierung bei 220 MHz)

5 Elem. DUT Yagi => 24 ... 20 Segmente (EZNEC Auto Segmentierung bei 340 MHz)

5 Elem. DUT Yagi => 43 ... 36 Segmente (EZNEC Auto Segmentierung bei 620 MHz)

  Welcher RL Plot repräsentiert nun die wahre Kurve des Plot für eine Aufbau ohne Boom als Basis um den BC aufzusetzen?

Herleiten der SBC-Komponente

Es ist also von grundlegender Bedeutung die passende Segmentierungsdichte die mit der betrachteten Antenne korrespondiert zu finden - oder besser gesagt - dem Weg, wie der NEC Kernel mit den in das Antennenmodell eingeschlossenen Herausforderungen umzugehen vermag. Um den Einfluss der Segmentierungsdichte des Modells in die BC Theorie mit einfließen zu lassen habe ich die Komponente "Segmentierungs BC" (SBC) vorgestellt (s. "Applied Conversion of Segmented Wires from NEC to 144 MHz Yagi Elements" - Teil 1, Dubus 2/2010 und folgende). Das ist jetzt keine Aufgabe an den BC im klasischen Sinn. Traditionelle BC-Werte sind dafür gedacht, auf eine Yagi angewandt zu werden, die als realer Aufbau ohne Boom bereits exakt auf der richtigen Frequenz liegt. Der SBC hilft, Drähte aus NEC in echte Aufbauten zu überführen. Dieser zusätzliche SBC vermittelt zwischen nicht passender Segmentierungsdichte und einer zum echten Aufbau ohne Boom passenden Dichte indem der Unterschied zwischen den Resonanz-Peaks beider Modelle ermittelt wird. Dieser Betrag ist äquivalent zu einer Extraportion BC in Millimetern.

Damit bringt der SBC etwa zustande, was beim Anwenden von beispielweise DL6WU/G3SEK Werten auf beliebige Modelle oft nicht erkannt wird, weil die Genialität des DL6WU als Lösung sämtlicher Probleme angesehen wird.

Man rechnet das Modell zweimal durch. Einmal mit der bei der Entstehung des Designs angewandten Segmentierungsdichte; die Frequenz des Resonanz-Peak wird notiert. In einem zweiten Durchgang wird die dem Aufbau ohne Boom entsprechenden Segmentierungsdichte angewandt; wieder wird die Frequenz des Resonanz-Peak notiert. Nun bildet man die Differenz der beiden notierten Frequenzen und multipliziert diesen Wert mit dem unten angegeben Faktor um die zusätzlichen Millimeter zu gewinnen, die in diesem Fall zu dem normalen BC addiert werden müssen.

Wie kommt das - und welches Vorzeichen muss die mittels SBC ermittelte Korrekturlänge besitzen?

Hier müssen wir einmal um die Ecke denken. Nehmen wir an, das ein Designer davon überzeugt ist, das eine Segmentierungsdichte, die um einiges höher liegt als das, was tatsächlich der Testantenne ohne Boom entsprechen würde, eine gute Wahl sei. So entwirft er also seine Antenne mit der Konsequenz, das durch die höher gewählte Segmentierungsdichte die Elemente gleicher Länge jetzt bei der Berechnung den NEC Kernel länger erscheinen als bei der zutreffenden Vergleichsdichte. Daher wird der Designer alle Elemente ein wenig kürzer wählen um mit einem Simulationsmodell abzuschließen, das einen SWR-Verlauf wie geplant besitzt. Wenn wir dies Modell jetzt mit der dem echten Aufbau ohne Boom entsprechenden Segmentierungsdichte simulieren, so wird als Ergebnis ein höher in der Frequenz liegender Resonanz-Peak errechnet. Der echte Aufbau mit dieser Geometrie läge um eben diesen Frequenzunterschied zu hoch. Das korrigieren wir, indem wir den richtigen SBC-Wert in Millimetern zur Elementlänge zufügen. Im umgekehrten Fall einer mit weniger Segmenten entworfene Yagi müsste dieser SBC-Wert abgezogen werden.

---

Der SBC .......... Segmentation Density (Boom) Correction

  Wie anwenden?

Der SBC wird auf den normalen BC aufgeschlagen

Wie kommt man an die Zahlenwerte?

Die beiden Faktoren, die Segmentierungsdichte der echten Yagi ohne Boom und der Faktor um den SBC in Millimeter umzurechnen, müssen aus echten Messungen gewonnen werden. Für eine konventionelle Yagi, also mit geradem, gestreckten DE ohne nach Art einer Quad oder scharf gebogenen Elementen ist die Segmentierungsdichte für die Yagi und so der Wert des SBC ohne Boom recht dicht an der Segmentierung, die man erhält, wenn die EZNEC Autosegmentierungsfunktion für die vorgesehene Designfrequenz angewandt wird. Das sind dann ungefähr 11 Segmente angefangen mit dem Reflektor und fallend auf etwa 9 für die letzten Direktoren. Für eine Yagi mit gespeister Schleife als erregtes Element wie die LFA nach G0KSC sind das etwa 30+ Segmente, was mit einer EZNEC Autosegmentierung bei rund 420+ MHz vergleichbar ist.

Multiplikationsfaktoren um den SBC in Millimetern zu berechnen

Freq. [MHz]     Factor [mm/MHz]
    50               16.00        (rechnerisch)
    70               12.50        (rechnerisch)
   144                5.85
   222                2.86        (rechnerisch)
   403                1.02        (rechnerisch)
   432                0.92
   1296               0.196
 

(Die Zahlen oben sind die reziproken Werte von dem, was ich
in MHz/mm in der Dubus Artikelserie zum BC publiziert habe)

Beispiel:

  Hoch segmentierte 144 MHz Yagi mit bestem RL bei 144.3 MHz,
  Autosegmentiert bei 144.1 MHz => bestes RL verschiebt sich zu 144.7 MHz
  SBC = delta Freq. * Faktor = 0.4 MHz * 5.85 mm/MHz = 2.3 mm


Übersicht: Längenkorrekturwert Yagi-Element, per MHz/mm in einem Diagramm

basically tested
fully tested



Übersicht: Längenkorrekturwert Yagi-Element, per MHz/mm in einem Diagramm - 0 ... 500 MHz

Übersicht: Längenkorrekturwert Yagi-Element, per Kehrwert mm/MHz in einem Diagramm

  Wenn wir den SBC nicht mit einschließen, sondern die Yagi durch Veränderungen an DE und D1 hin trimmen ... können wir schließlich eine Yagi bekommen, die ein niedriges VSWR hat, wo wir es haben wollen. Allerdings werden dann sämtliche Direktoren um den Betrag des SBC zu kurz geraten sein. So daß dadurch, und die Manipulationen der Erregerzelle weder das Strahlungsdiagramm noch die Werte für Gewinn, F/B oder Antennentemperatur genau wie simuliert ausfallen werden.

---

Einige Permittivitätswerte

Material     bei        1 MHz       3 GHz

Bienenwachs             2.53       2.39
Silikon                11.7-12.9
Silikon RTV             3.6
Gummi                   3.0-4.0
Butyl-Gummi             2.35       2.35

ABS                     2.0-3.5
Bakelit                 3.7
Delrin (R) Harz        3.7
Kapton (R)             3.9 - 2.9
Nylon                  3.2 - 5
Acrylglas              2.2-3.4
LDPE & HDPE            2.26        2.26
PA                     2.5-2.6
Polycarbonat           2.8-3.4
PP                     2.2
PVC                    3
PTFE                   2.0-2.1


Epoxy PCB               5.2
FR4 PCB                 4.9        4.2
RT PCB                  2.2

Wasser                ~ 80 at 20 C
Eis (Dest. Wasser)     4.15        3.2

---

DG7YBN Yagi Elemente Konfigurations-Tool

Seit Version 1.32 hat dieses Werkzeug eine eigene Seite: klick hier

Alte Ausgabe:

Dies MS Excel Tool ist die Nachfolge-Software für mein On-Boom-BC Excel. Die aktuelle Versionsnr. ist 1.51
Es enthält eine Reihe von neuen Möglichkeiten wie Import von .NEC Dateien, eine Datenbank, DL6WU BC, Hilfe-Schaltflächen.

Erstmals ist die Sprache sämtlicher Hilfetexte und Pop-Up Fenster umschaltbar Englisch / Deutsch ausgeführt.

DG7YBN Yagi Element Configuration Tool, Vers 1.51

Key Features

• Berechnet BC nach DL6WU, SM5BSZ und DG7YBN für Elemente auf dem Boom
• Amateurbänder 50 bis 432 MHz
• Import von .nec Dateien wie von 4nec2
• Datenbank, welche als CSV-Datei importiert / exportiert werden kann
• Beta-Version eines Windlastrechners für Yagis
• Es ist getestet mit MS Excel 2003 auf winXP, MS Excel 2007 auf winXP, MS Excel 2010 auf win7

Es ist getestet mit MS Excel 2003 auf winXP, MS Excel 2007 auf winXP, MS Excel 2010 auf win7.

Leider sind win98, win2000 und Excel aus dem 97 MS Office nicht unterstützt.

Die MS Excels Sicherheitseinstellungen müssen so gesetzt sein, dass sie das Ausführen von Makros erlauben,
denn der Visual Basic Code enthält mittlerweile über 8000 Zeilen.

Haftungsausschluss: Diese Excel enthält Makros.
Bitte nur Downloads aus einer sicheren Quelle benutzen; die Benutzung ist in jedem Fall auf eigenes Risiko (!)

Um das gezippte Tool herunterzuladen, bitte zur Seite des Tools wechseln


Hinweis: Die auf dieser Website genannten und gezeigten Logos, Bezeichnungen, Warenzeichen und Markennamen
sind Eigentum der entsprechenden Firmen und unterliegen dem Markenrecht!

---

73, Hartmut, DG7YBN